Άσκηση: Κανονική Κατανομή
Η ετήσια αρδευτική κατανάλωση νερού μιας αγροτικής περιοχής είναι 60 MCM. Η περιοχή αρδεύεται από ταμιευτήρα χωρητικότητας 65 MCM στον οποίο η ετήσια εισροή έχει μέση τιμή 80 ΜCM και τυπική απόκλιση SD=20.
Να απαντηθούν τα πιο κάτω με την χρήση του διαγράμματος πυκνότητας πιθανότητας:
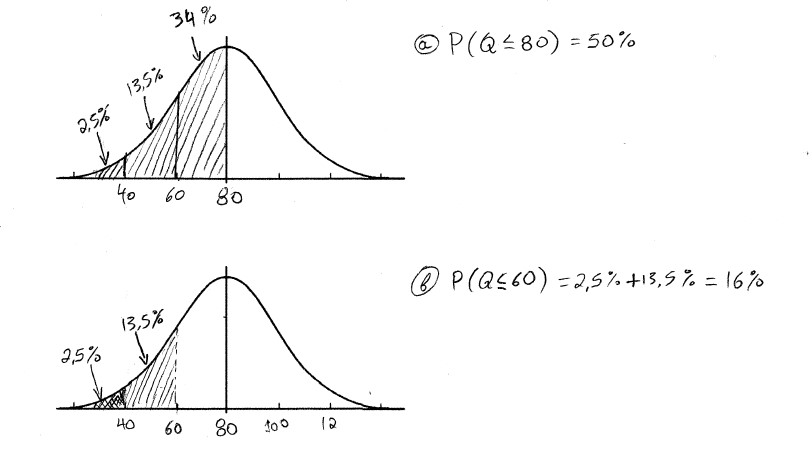
α) Ποια η πιθανότητα η ετήσια εισροή στον ταμιευτήρα να είναι ίση ή μικρότερη από 80 MCM;
β) Ποια η πιθανότητα η ετήσια εισροή στον ταμιευτήρα να είναι ίση ή μικρότερη από 60 MCM;
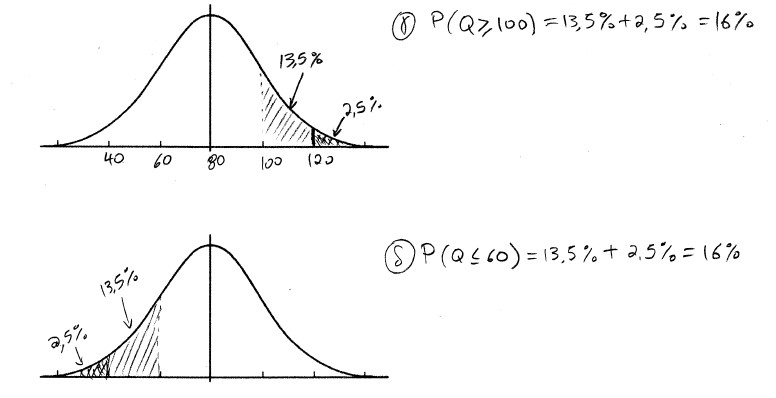
γ) Ποια η πιθανότητα η ετήσια εισροή στον ταμιευτήρα να είναι ίση ή μεγαλύτερη από 100 MCM;
δ) Ποια η πιθανότητα η ετήσια εισροή στον ταμιευτήρα να είναι ίση ή μικρότερη ετήσιας αρδευτικής κατανάλωσης, δηλαδή των 60 MCM;

Επεξηγηματικές σημειώσεις
Η ετήσια εισροή είναι μια τυχαία μεταβλητή. Δηλαδή δεν μπορούμε να ξέρουμε εκ τον προτέρων τι τιμή θα έχει. Το μόνο που μπορούμε να κάνουμε είναι να την μετρούμε κάθε χρόνο για να καταλάβουμε που περίπου κυμαίνεται. Με τις μετρήσεις βρίσκουμε την μέση τιμή, την τυπική απόκλιση κτλ. Έτσι, μπορούμε να υπολογίζουμε ποια είναι η πιθανότητα η μεταβλητή μας να πάρει τιμή μεγαλύτερη ή μικρότερη από μια συγκεκριμένη τιμή. Στην Διαχείριση Υδατικού Πόρων μας ενδιαφέρει ιδιαίτερα να γνωρίζουμε την πιθανότητα γιατί μας επιτρέπει να υπολογίζουμε την πιθανότητα να έχουμε το νερό που χρειαζόμαστε για συγκεκριμένη χρήση.
Στην περίπτωση της άσκηση αυτής, έχουν γίνει κάποιες μετρήσεις και γνωρίζουμε ότι η ετήσια εισροή ακολουθεί κανονική κατανομή και έχει μέση τιμή μ=80 MCM και τυπική απόκλιση SD=20 MCM. Γνωρίζοντας αυτά μπορούμε να χρησιμοποιήσουμε τον πίνακα της κανονικής κατανομής για να υπολογίσουμε πόση είναι η πιθανότητα η μεταβλητή μας να είναι μικρότερη από κάποια τιμή.
Στο μάθημά μας, για ευκολία, αντί του πίνακα δώσαμε έμφαση στην γραφική απεικόνιση της πιθανότητας στο διάγραμμα της πυκνότητας πιθανότητας. Συγκεκριμένα ασχοληθήκαμε μόνο με την πιθανότητα συγκεκριμένων τιμών (μ, μ-SD, μ+SD, μ-2∙SD, μ+2∙SD) των οποίων η πιθανότητα αντιστοιχεί στα εμβαδά που φαίνονται πιο κάτω
Λύση: Η ζητούμενες πιθανότητες δίνονται αθροίζοντας τα αντίστοιχα εμβαδά. Ακολουθεί επεξήγηση στην σελίδα 2