Ανάλογα με τις συνθήκες που επικρατούν σε ένα υδροφορέα, το νερό μπορεί να είναι στάσιμο ή να κινείται. Συνήθως η ροή του νερού είναι της τάξης των μερικών μέτρων ανά ημέρα. Σε πολλές περιπτώσεις, μας ενδιαφέρει να γνωρίζουμε την κατεύθυνση και την ταχύτητα αυτής της ροής. Πχ.:
- Για τον υπολογισμό των διαφυγών από ένα υδροφορέα.
- Για τον υπολογισμό του υδατικού ισοζυγίου.
- Για την εκτίμηση των δυνατοτήτων άντλησης από ένα υδροφορέα.
- Για την εκτίμηση της διάδοσης μιας ρύπανσης στο νερού
Για μονοδιάστατη ροή (στο επίπεδο x-y) μπορούμε να χρησιμοποιήσουμε το νόμο του Darcy για να εκτιμήσουμε την ειδική παροχή qx
Νόμος του Darcy: Η ειδική παροχή είναι γραμμικά ανάλογη της υδραυλικής αγωγιμότητας K και της υδραυλικής κλίσης.


qx = Ειδική Παροχή. Είναι η παροχή (Q) ανά μονάδα επιφάνειας (Α). Έχει διαστάσεις ταχύτητας, συνήθως m/day.
K = Υδραυλική αγωγιμότητα. Συντελεστής που εξαρτάται από το πόσο εύκολα περνά το νερό μέσα από τον εδαφικό σχηματισμό. Έχει διαστάσεις ταχύτητας, συνήθως m/day.
dh/dx= υδραυλική κλίση. Με απλά λόγια, πόσο απότομη είναι η διαφορά υδραυλικού ύψους μεταξύ δύο θέσεων. Αδιάστατο.
Υπάρχει πλην επειδή η κατεύθυνση της ροής είναι προς τα εκεί που μειώνεται το υδραυλικό ύψος (αρνητική υδραυλική κλίση).
Ταχύτητα ροής
Η ειδική παροχή qx έχει την έννοια της παροχής ανά μονάδα επιφάνειας κάθετης στην διεύθυνση [m3/s] / [m2], γι’ αυτό και η μονάδα μέτρηση της είναι μονάδα ταχύτητας [m/s]. Η ειδική παροχή qx δεν αντιστοιχεί στην ταχύτητα ροής. Αυτό συμβαίνει γιατί στην μονάδα επιφάνειας περιλαμβάνονται κόκκοι του εδάφους και διάκενα. Η ροή όμως είναι μόνο διαμέσου τον κενών. Οπότε η ταχύτητά ροής διαμέσου είναι:

Όπου n το πορώδες του εδαφικού σχηματισμού.
Άσκηση: Οι απώλειες από τη λίμνη Α (αριστερά) τροφοδοτούν την λίμνη B (δεξιά). Η απόσταση μεταξύ τους είναι 3.5 km. Η στάθμη του νερού στην λίμνη Α είναι στο +1100 m και στην λίμνη Β στο +1060 m. Κ=12.5 m/day και n=15%.
Υπολογίστε την ειδική παροχή (qx) και την ταχύτητα ροής διαμέσου των πόρων
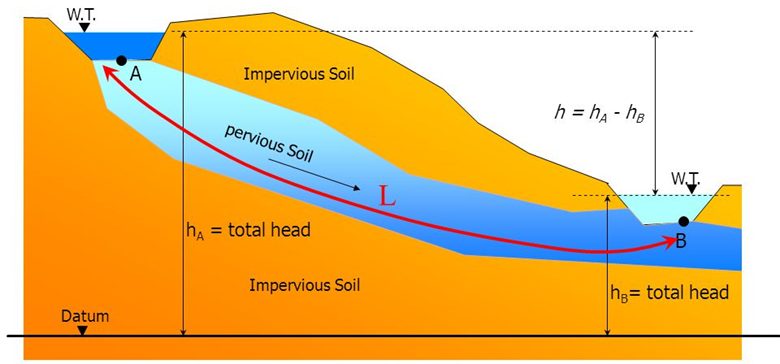
Υδραυλική κλίση: – dh/dx=-(1060-1100)/3500=-(-40)/3500= 0.0115
Ειδική Παροχή q=-Kdh/dx=12.5×0.0115=0.143 m/day
u_x=q_x/n=0.143/0.15=0.95 m/day
6.3.3. Διαφυγές υδροφορέα προς την θάλασσα
Συχνά, οι υδροφορείς που βρίσκονται σε παραθαλάσσιες περιοχές έχουν διαφυγές προς την θάλασσα. Στην πιο κάτω εικόνα, φαίνεται το θερμογράφημα μιας παραθαλάσσιας περιοχής. Με κόκκινο χρώμα, ξεχωρίζει η περιοχή όπου ρέει νερό από υδροφορέα που έχει υπόγειες διαφυγές προς τη θάλασσα. Γενικά, αναλόγως την εποχής, το νερό του υδροφορέα είναι είτε πιο ζεστό είτε πιο κρύο από το νερό της θάλασσας.

Άσκηση: Στο σχήμα δίδονται τα χαρακτηριστικά ενός υδροφορέα.
– Μέσο πάχος στην έξοδο 3 m
– Μέσο πλάτος υδροφορέα: 1,5 km
Υπολογίστε τον όγκο νερού που ρέει προς την θάλασσα

Υδραυλική κλίση dh/dx=2/1000=0.002
Ειδική Παροχή qx = 40 x 0.002 = 0.08 m/day
Διαρροή Qδ = 1500 x 3 x 0.08 = 360 m3/day
Ποια είναι η ταχύτητα ροής του νερού στους πόρους; Έστω n=30%
u_x=q_x/n=0.08/0.30=0.27 m/day
6.3.4. Πιεζομετρικοί χάρτες
Οι πιεζομετρικοί χάρτες δείχνουν το υδραυλικό ύψος στον υδροφορέα. Κατασκευάζονται χρησιμοποιώντας μετρήσεις του υψόμετρου της ελεύθερης επιφάνειας του νερού σε πηγάδια παρακολούθησης.
Ισοπιεζομετρικές καμπυλες: είναι οι καμπύλες ίσου υδραυλικού ύψους. Σε φρεάτιος υδροφορείς το υδραυλικό ύψος συμπίπτει με το υψόμετρο του υδροφόρου ορίζοντα
